The three Giza pyramids are located at 30° North, within an arcminute. (1)
The sides of the Great Pyramid point North within two or three arcminutes. (2)
Its slope angle is closely one-seventh of a circle, i.e. 51.4°.
More exactly, it is given A when cosA = 1/Φ where Φ is the golden ratio. So slope angle is 51° 50'.
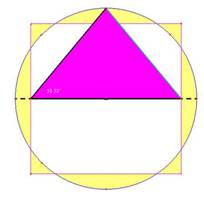
A 'golden triangle' defines the slope angle, with sides 1 for the base, √Φ for its height and Φ for its long side (hypotenuse); thus its sides increase or 'grow' in the same proportion.
We may write the 'Pythagoras' theorem' of this right-angled triangle as, Φ2 = Φ +1. That was two thousand years before Pythagoras.
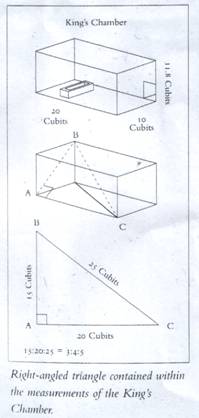
Diagram reproduced with permission from Heaven’s Mirror by Graham Hancock and Santha Faiia
This implies, that the square on the height equals the area of a pyramid side. To make a replica of the Great Pyramid, draw a 'map' where two golden rectangles are added to each of the four sides, and the pyramid sides drawn as triangles upon them.
The slope angle is also such that tan A = 4/л, i.e. the square on the base has length equal to that of a circle perimeter, whose radius equals the pyramid height: 51° 51'.
Thus phi and pi are integrated at this unique slope-angle. The four sides in fact concur within about an arcminute, on this slope angle.
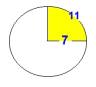
The pyramid height is 280 royal cubits and its base 440, so base to height are in the ratio 11 to 7 – an early expression of the л- ratio? Here, tanA = 14/11 giving 51° 51.'
The 'King's Chamber' has its length twice its breadth and its height is half the diagonal of that rectangle.
Taking the width of this chamber as unity, phi Φ is traced out by the height plus half the width.
A 3:4:5 Pythagoras triangle is contained in the diagonal plane of this otherwise-empty chamber: if its length is 4 units, the main diagonal is 5 and the diagonal across the end wall, 3.
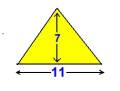
The actual size of this integer Pythagoras triangle in the King's Chamber establishes the units used for the Great Pyramid's exterior; the triangle sides being exactly 20, 15 and 25 royal cubits.
Flinders Petrie proposed that the adjacent 'Khafre' pyramid at Giza had its slope angle defined by the 3-4-5 triangle (3). Wikipedia cites this mean slope angle as 53°10', and arcsin (4/5) = 53° 8' (i.e., the angle whose sine is 0.8) – so this modern estimate of the mean slope angle of 'Khafre' lies within a couple of arcminutes of that 3-4-5 triangle base-angle.
The third Giza pyramid of 'Menkaure' has a slope angle estimated as 51° 20' (again, from Wikipedia) much closer to the 1/7th angle, which is 51° 25'. The three Giza pyramid slope angles seem to cluster around this value. The significance of this angle is confirmed by the way the ascending and descending passages of the Great Pyramid each form just half of that angle to the horizontal, so that there is a 1/7th angle between them. (4)

Summarising, the sublime geometry of this building integrates л and Φ as follows: its height is the radius of a circle whose circumference equals the base perimeter, and its height is the side of a square whose area equals that of each of the four sides.
The 'Seked'
Pythagoras' theorem was used in defining the Great Pyramid geometry, the earliest record of its use, but this is ignored or dismissed in histories of mathematics. The philosophical meaning of the coming together of the two transcendental terms pi and phi in the Giza slope angle is well discussed in John Ivimy's The Sphinx and the Megaliths (1974). A slope angle as defined by a 3:4:5 triangle (Khafre) is something you or I might dream up, whereas the pi/phi concordance and the one-seventh slope angle of the Great pyramid seems more, kind of – divine.
Ancient Egyptian texts lack any concept of an angle, but do have the 'seked.' This seked was a ratio, that between half the base-side of a pyramid and its height. That is the cotangent of our angle 'A': thus the 'seked' of the Great Pyramid was л/4, while that of the adjacent Khafre pyramid was 3/4. (5) Wonderfully, this Seked value of the Great Pyramid is equal to
1 – 1/3 + 1/5 -1/7 + 1/9 – 1/11… etc.
a series which goes on forever, using all the odd numbers (Leibniz found it in 1674).
'Herodotus wrote that the pyramid was built so that the area of each lateral face would equal the area of a square that had one side as long as the pyramid was tall.' (6) Whether Herodotus ever wrote such a thing seems doubtful (7), but that remark is widely quoted! This gives us the ratio pyramid height / half base-length equal to √Φ. (8) The 'Seked' (i.e., cotA, as in (5) and (6) above) here equals 1/√Φ.
Maybe Thoth-Hermes understood these things, long ago.
Half of the Base Area
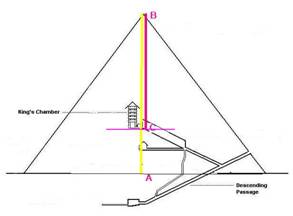
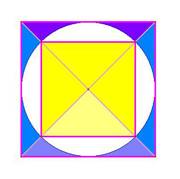
The King's chamber, as William Petrie pointed out in 1883, 'was placed at the height in the Great Pyramid at which the area of the horizontal section is equal to one-half the area of the base'. (9) That height implies use of the square root of two – how exact was that?
In the figure,
√2 = AB / BC
Where the height of the pyramid AB is 280 cubits = 146.64 metres (its theoretical height, as if it still had the capstone), and the height of the floor of the King's Chamber floor AC is 82.09 cubits = 42.99 metres (10). That equation would then be exact to 99.8%. That has to be intentional. Experts have surmised that the King's Chamber floor height was intended to be just 82 cubits, (11) which would make this ratio exact to four figures! Thus the scale chosen for the building made the units of measure used chime in with this 'irrational' ratio, 1.414…
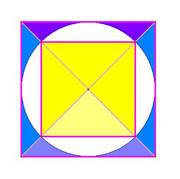
The Victorian astronomer Richard Proctor wrote a book proposing that the Great Pyramid was first only half-built, up as far as what became the King's Chamber floor. So, this has been regarded as quite an important juncture. (It was then used as an observatory, he argued). He did not comment upon its exact mathematical placement. The yellow square in the diagram represents this floor at the King's Chamber level, and this may be a good visual method of 'seeing' the root two relationship, whereby it is half the area of the outer square, which represents the base. (12)
* Half of an Angle
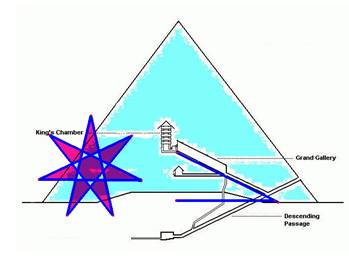
The Ascending Passage leading up to the 'King's Chamber' has a slope angle of 26° 2' (13). This angle bisects that of the Great Pyramid's outer slope angle, within arcminutes. Therefore, this slope angle represents a one-fourteenth division of a circle. This mysteriously re-emphasises the number seven, within the Great Pyramid. The lovely star-heptagon (see figure) has this angle at its corners.
If those who built this pyramid were able to bisect a one-seventh angle within arcminutes, that would tend to indicate their use of angular measure.
Notes:
- This 1' error may have been due to atmospheric refraction: Peter Lancaster-Brown, Megaliths, Myths and Men, 1976, p271. 'The apparent (not true) altitude of the pole is 30° 00' (1/12 of a circle) as seen from all three Giza pyramids:' Dio, a history of astronomy journal, Baltimore, Dec. 2003. Hugh Thurston, 'Orientation of Early Egyptian Pyramids', p.6. [back to text]
- For comparison, the adjacent Khafre pyramid points due North with an error of about 6', but in the other direction, possibly indicating a later construction. [back to text]
- Petrie wrote, 'Here there can scarcely be any doubt that the 3:4:5 triangle was the design for the slope.' [back to text]
- Discussed by Robin Heath in Sun, Moon and Stonehenge, 1998, p.178. [back to text]
- In the Rhind Papyrus, c. 2000 BC: Eli Maor, Trigonometric Delights (Princeton, 1998). [back to text]
- The Joy of Pi, David Blatner, 1997 p.11. Blatner errs in saying that this definition gives pi, rather than phi. [back to text]
- The History of Herodotus, Trans. Rawlinson, NY,1936, Book II, p.125. [back to text]
- We can write 'Herodotus' condition' as h2 = l√(h2+l2) where l is half the base length and h the pyramid height. Mathematically-inclined readers will solve this, to obtain h/l = Φ, because Φ = (1+ √5)/2. [back to text]
- W.M.F. Petrie, The Pyramids and Temples of Gizeh (London, 1883), 186-7. Graham Hancock, Fingerprints of the Gods, 1995, p.358. [back to text]
- Data from www.repertorium.net/rostau/measures.html; [back to text]
- See John Legon, www.legon.demon.co.uk/greatpyr.htm [back to text]
- See William Glyn-Jones on GH Forum, http://www.grahamhancock.com/forum/GlynJonesW3.php?p=10 [back to text]
- Hancock, Fingerprints, p.337. [back to text]