A new book released November 2006 is set to challenge the position of orthodox Egyptology by presenting a new paradigm for the pyramids of Giza. Entitled, The Giza Oracle, by independent researcher and writer, Scott Creighton, it presents a simple yet compelling solution to the mystery of the Giza Pyramid alignments and goes on to demonstrate how all 11 pyramids along with the Great Sphinx form a grand `Precession Wheel’, indicating key dates from humankind’s remote past – and, indeed, its future. In addition the book demonstrates links between Giza, Teotihuacan in Mexico, Xi’an in China and – peculiarly – the site of Rosslyn Chapel in Scotland.
It is only in relatively recent times that we have begun to view the Great Pyramids of Giza not as individual monuments but as part of a much larger scheme, a unified design. This concept was first proposed by the American architect J.A. Kane in a thesis entitled, “The Ancient Building Science.” In his thesis Kane argues that the 3 Giza pyramids formed a single, unified master plan based upon geometrical and surveying principles derived from astronomical observations. Alas, Kane’s ideas fell on deaf ears and the baton was picked up by the Egyptologist, Mark Lehner of Yale University. Although Lehner’s study of the Giza site from 1984-1986 limited itself to the site’s geomorphy, he later reported that there exists at Giza an obvious diagonal alignment that touches the south-east corner of all 3 pyramids. This became known as the `Lehner Line’.
The idea of a unified master plan of Giza was progressed still further by the academic, John Legon, whose paper was published in 1979 in the Reports of the Archaeology Society of Staten Island and also the Oxford Journal, Discussions in Egypt. Legon’s work was of an intensely mathematical nature and demonstrated that the spatial relationship between the Giza 3 could not have arisen purely by chance alone.
Arguably the most widely-known unified design theory was that presented in 1994 by the writers Robert Bauval and Adrian Gilbert in their ground- breaking book, The Orion Mystery: Unlocking the Secrets of the Pyramids. In their book, Bauval and Gilbert present a theory whereby, circa 10,500BC, the Giza 3 were unified through an alignment with the 3 stars that form Orion’s Belt. Uniquely, however, the `Orion Correlation Theory (OCT)’ as it came to be known, attempted also to incorporate cultural and religious evidence as a main plank of the theory. Although today there are sceptics of this theory, the arguments still go on and will most likely continue to do so. In one way the theory presented in The Giza Oracle makes a return to the mathematical/astronomical proposals of the earlier researchers but with one major difference. Whereas other writers credited the Ancient Egyptians with the Giza design, the starting point for The Giza Oracle assumes that such designs for the plateau came from a much earlier, pre-dynastic time; a time before any cultural or religious beliefs had even formed. There are some hints that plans did indeed exist in the most ancient times.
“The design of the structures that Imhotep raised for Djoser at Saqqara seems to hark back to a remote past, deliberately recalling the occasion of the `First Time’, when creation arose in the primeval marsh, to which Djoser would return on death.”
Regarding other temples such as Edfu and Denderah (with its astronomical clock):
“They (the temples) were built according to an architectural plan which was supposed to have been revealed in a codex that fell from the heavens at Saqqara in the days of Imhotep.”
Although the Giza complex may not actually have been designed by the Ancient Egyptians of the 4th Dynasty, it should be made clear, however, that it is to those people that credit for implementing the ancient design and actually constructing the Giza pyramids must be given.
The other main difference with earlier researchers is that The Giza Oracle presents a theory that incorporates all the structures on the Giza plateau (the 11 pyramids and the Great Sphinx) as forming part of an ancient mathematical/astronomical calendar that reveals key dates from the most ancient past. When comparing these dates with known scientific data of these times, it seems almost as if the ancients are attempting to draw our attention to them – as though there is a message for future generations to learn by looking to the past.
The fact that the structures of the Giza plateau are – when compared to other temples and burial chambers in Egypt – quite devoid of inscriptions, seems almost as though they have been purposefully left in this state perhaps in order that they can `communicate’ to us in a much more basic and universal language – the language of mathematics. There are no inscriptions of any great number or significance inside or outside any pyramid here; nothing that could distract from or blur the `message’. One possibility for this glaring lack of inscriptions at Giza is perhaps because it had been ordained in the ancient design that the site should not carry any such `distractions’. When one views the Giza plateau from any distance, what one immediately recognises is the geometry and symmetry of its structures – in other words, the language of mathematics. By considering the plateau in this way it seems natural that the primary context of the Giza monuments is mathematical.
And, of course, there are clear benefits for the Designers of the plan to have chosen the language of mathematics to communicate any `message’ since only in this language could they ensure the essence of what they are trying to say would be preserved – no matter how long the passage of time. Mathematics is not ethnocentric and transcends all times and cultures – past, present and future. Certainly the level of mathematical understanding will differ across the ages and within different cultures, for example, the understanding of abstract numbers such as Pi and Phi. Quite simply, however, to any society reasonably advanced in mathematics and astronomy, this discipline would be the `language’ of choice to preserve and `transmit’ important information far into the future where meaning – if written as text or in some form of hieroglyph – might otherwise be misinterpreted or corrupted. In short, the meaning in any text can become lost in translation – mathematics remains pure.
This is not to say, of course, that the ancient Designers would have used complex or convoluted mathematical formula to encode their information since this would be totally counter-productive. If the key requirement is – first and foremost – to transmit information in such a way that it can be easily understood, then it stands to reason that it should not require a mathematical genius to detect and decode it.
And so, in this regard, the use of such obvious numbers would be critical to signalling a `message’. Unlike purely arbitrary or random numbers, significant mathematical numbers would stand out like a beacon and stimulate the curiosity of other advanced cultures that happened to recognise them to investigate further. Such a mathematical beacon would be akin to our own civilisation receiving a radio signal containing a long, repetitive sequence of Prime Numbers from deep space as in the popular Hollywood movie, Contact. The first clue (or mathematical beacon) indicating that there is a possible mathematical significance to the Giza monuments seems straightforward enough and comes from the most fundamental and obvious mathematical function of all, Pi (3.14…).
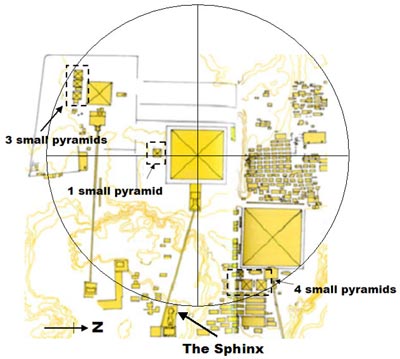
Figure 1 – The Great Giza Circle – The `Secondary Pyramids’ Hint at Pi (3.14) Map Source, Lehner – `The Complete Pyramids’
As can be seen in figure 1, the eight so-called `secondary pyramids’ (which includes the recently discovered remains of the Cult pyramid of Khufu) hint at the mathematical function, Pi (3.14). In turn, Pi indicates a circle. It seems reasonable and logical to assume that this `Great Giza Circle’ should be drawn outwards from the centre of the middle pyramid (Khaf-Ra) until all pyramids on the plateau are enclosed within it. Notice, however, that by enclosing all the pyramids precisely within the Great Giza Circle, the Great Sphinx remains fractionally outside it. There is a very specific reason for this arrangement, which we will return to later.
Placing Pi so clearly within the design acts almost like a beacon from the Designers that the context of their `blueprint’ is fundamentally mathematical in nature. However, this raises an important question – does this then show that the Ancient Egyptians themselves understood the mathematical concept of Pi? Opinions vary on this question with some scholars believing they did and others claiming otherwise. Of those who believe the Ancient Egyptians did indeed understand Pi, they have no evidence that tells us how the Ancient Egyptians might have noted it e.g. 22/7, 3 and 1/7 or 3.14. With no supporting evidence, the fact that we can so easily observe 3-1-4 in the design is, in all likelihood, a matter of simple coincidence.
Or – is it perhaps possible that the observance of a simple 3-1-4 in the Giza structures is indeed a beacon from a civilisation that perhaps existed long before dynastic Ancient Egypt – a `lost civilisation’ that did indeed understand Pi in the form 3-1-4? A civilisation that perhaps created the ancient codex received at Saqqara in the mythical `First Time’? Speculation, of course, and we will never know this for sure. What can be said for certain, however, is that over the ages knowledge can be gained and lost again and it is likely that this has occurred many times in the development of civilisation. The fact remains, however, 3-1-4 is easily observed in the secondary pyramids of Giza and may – or may not – be the result of simple coincidence.
The first part of The Giza Oracle attempts to demonstrate a simple mathematical solution to the age-old puzzle of the so-called `misaligned’ Pyramid of Menkau-Ra, the smallest of the 3 main pyramids at Giza. Bauval and Gilbert speculate that this correlates with the `misaligned’ star of Orion’s Belt with the Nile mirroring the Milky Way. The hypothesis presented by Bauval and Gilbert does not, however, impinge on the hypothesis being presented in The Giza Oracle, which places the Giza `masterplan’ as having been conceived in the pre-dynastic era before any such religions were practiced.
The problem of finding a mathematical solution to the pyramid alignment puzzle presents itself with little difficulty and utilises what has come to be known as the Giza Centroid Alignment Theory or (CAT). This theory had its origins in considering the puzzle of the very unusual `bisectors’ in the pyramids of Khufu and Menkau-Ra (figure 2).
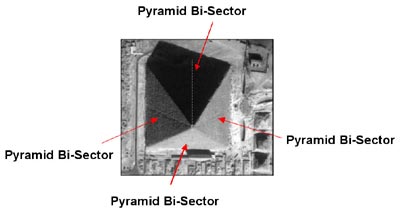
Figure 2 – Ikonos satellite image of the Great Pyramid
The `bisectors’ of Khufu and Menkau-Ra are 8 lines (4 in each pyramid) that run vertically through the centre of each face of these 2 pyramids, which are formed by the angled arrangement of the stone blocks. What could these 8 lines mean and why should they be found only on the faces of these 2 pyramids?
A possible and surprisingly simple mathematical answer was quickly discovered. Unlike a square or circle, a triangle that is not equilateral has many centres known as `centroids’. Each of these different centroids or `points’ within the triangle satisfies some unique property. Our modern mathematics is aware of over a hundred different triangle centroids but it seems the ancients knew how to plot only the three simplest of these: Incentre, Centroid and Circumcentre. The ancient Greeks, however, added a fourth triangle centroid known as the Orthocentre. The three simplest and most ancient triangle centroids the Designers may have been familiar with are detailed below (figures 2a-2d).
Centre 1 – The `Incentre’
This point requires a circle to be inscribed within the triangle whereby the perimeter of the circle touches all three sides of the triangle. The centre of the inscribed circle is then plotted and this point becomes the triangle’s Incentre.
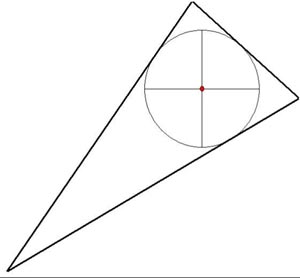
Figure 2a – `Incentre’
Centre 2 – The `Centroid’
This point requires a line to be drawn from each of the triangle’s vertices to the midpoint of the opposite parallel. The intersection where the lines meet is plotted and this point becomes the triangle’s Centroid.
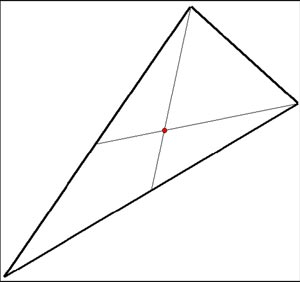
Figure 2b – `Centroid’
Centre 3 – The `Circumcentre’
This point requires a circle to be circumscribed around the triangle in such a way that its perimeter touches all three vertices of the triangle. The centre of the circumscribed circle is then plotted and this point becomes the triangle’s Circumcentre.
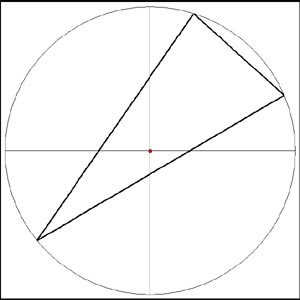
Figure 2c – `Circumcentre’
If we now overlay each of the three different centroids outlined above against a site plan of Giza, we arrive at an alignment of the 3 centroids that is a precise match with the centre points of the Giza Pyramids.
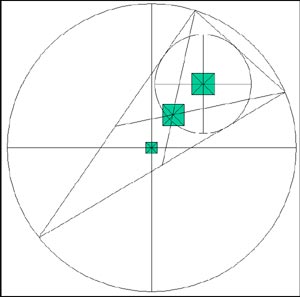
Figure 2d – The 3 Centroids align with the Pyramid Centres
Of course, the triangle used in the above example has been very carefully constructed in order to achieve an exact alignment of the 3 centroids with the pyramid centres. Indeed, no other triangle will offer 3 centroids that will exactly align with the pyramid centres. The main point of this design technique, however, is that it provides a possible means of explaining the 8, hitherto, mysterious centre lines of Khufu and Menkau-Ra which correlate precisely with the underlying plan (figure 3a).
It is entirely possible, however, to apply the technique described above retrospectively to any 3 pyramids in Egypt and arrive at a triangle of a particular dimension whose centroids would, as a result of the mathematical principles, naturally correlate with the centre of those 3 pyramids. This, therefore, shows no proof that this is the underlying design technique because it could not (of itself) demonstrate any intention on the part of the Designer in the use of this design technique.
However, what would most definitely not occur as a natural result of the mathematics (in addition to the 3 matching centres) is to find 8 lines in the `plan’ that also correlate with features in the physical pyramids! This could only occur if such features (lines) were intentionally `sculpted’ into the pyramids. That the physical lines in Khufu and Menkau-Ra exist and correlate perfectly with this design method is not questioned but was this done to `mimic’ the underlying design? Are we perhaps looking at coincidence again? Certainly, this is possible. However, there comes a time when one must decide where coincidence ends and conformity begins. In this case when divergent elements such as the 3 centroids and 8 bisectors coincide again and again and again with the relative positions of the 3 pyramids and the individual placement of the lines on the 4 faces of Khufu and Menkau-Ra, coincidence must surely subside to conformity. The question can be summarised thus: does the Centroid Alignment Theory offer us a reasonable explanation for the distribution of the pyramids in conjunction with the physical lines we observe in Khufu and Menkau-Ra? It is probably fair to say that it is possible.
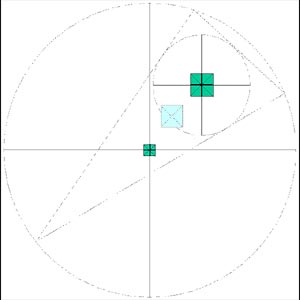
Figure 3a – The Incentre and Circumcentre of the GGT produces bisectors in Khufu and Menkau-Ra, dividing them into 8 sides
However, if the Centroid Alignment Theory is indeed the underlying design mechanism used by the Designers, it still does not explain why they would have chosen such a triangle as the basis for their design nor, indeed, does it explain the purpose of the bisectors. What we must keep foremost in our minds is the extraordinary amount of additional effort it would have taken to construct these two pyramids with these bisectors. Is this perhaps indicative that the pyramids of Khufu and Menkau-Ra have some unique or `special’ function to convey the ancient’s `message’. This may indeed be so as we shall discover shortly.
One possible significance for this design mechanism is to ensure the apex of the Great Giza Triangle is `pointing’ to a very specific location in the Egyptian desert (figure 3b).
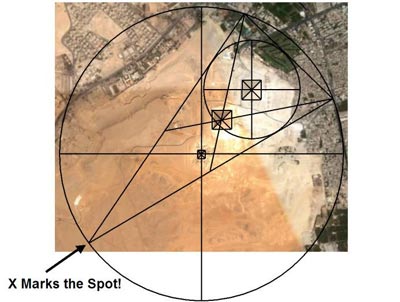
Figure 3b – Aerial Image of the Giza Plateau. The Apex of the GGT Converges at a Location Southwest of Menkau-Ra
What might be excavated and discovered under the sands at this location we can but speculate. The legendary `Hall of Records’? The lost Benben Stone of Heliopolis? The Ark of the Covenant? The 300 or so `lost’ Books of Enoch? Who knows? There may be nothing. However, only by careful excavation of this spot in the Egyptian desert can we ever hope to reveal the truth.
A more likely explanation for this particular design technique relates directly to the Great Giza Circle (figure 1) and the Sphinx and will be explained shortly.
In figure 1 it was explained how the secondary pyramids `hinted’ at Pi (3.14) and from this, a circle was circumscribed around all the pyramids, leaving the Great Sphinx just outside this circle. What are we to make of this circle? One possibility is to consider it as representing a `precession clock’ that utilises the zodiac. But which zodiac? The zodiac we use today, which has its roots in the Babylonian zodiac, is not the same zodiac used by the Ancient Egyptians. And it seems that if the Great Sphinx is symbolic of the Age of Leo then this is also a problem since there was no such sign or age in the Ancient Egyptian zodiac. This presents a significant problem since the Giza Precession Wheel Theory fundamentally relies upon the Great Sphinx (the Lion) as being symbolic of the former Age of Leo (circa 10,948BC). However, it seems that the Babylonians themselves somehow obtained their zodiac from some other `unknown’ source. In his thesis, `The Definition of the Babylonian Zodiac and the Influence of Babylonian Astronomy on the Subsequent Defining of the Zodiac’, Robert Powell PhD, writes:
“It is unknown through whom the innovation leading to the introduction of the zodiacal coordinate system into Babylonian astronomy took place.”
It is possible then, on the basis of this, that in a time before the Babylonians, someone, somewhere may have had the beginnings of our present zodiac – a zodiac that perhaps did include the Age of Leo, symbolised as a lion. Lost knowledge of a `lost civilisation’ perhaps?
Accepting this as a possibility the twelve signs of the zodiac are placed around the precession wheel to create a `precession clock’. The starting point or calibrating point for the wheel is, of course, the Great Sphinx and this possibly explains why it sits outside the circle – its realm is in the cosmos and the wheel is symbolic of the precessional turning of the stars. The date the clock is calibrated to is the dawn (symbolised by the Great Sphinx facing east where dawn rises) of the previous Age of Leo (the Sphinx symbolises a lion) which occurred around the year 10,948BC.
It is unlikely, however, that the ancient Designers of the Giza Precession Wheel would have left us to guess precisely what year they used as the start point for their astronomical clock and would have found a way to tell future civilisations the precise date to use as the start date – i.e. the year, relative to our own time-frame, the Designers' recognised as the 'Dawn of Leo'. This date will, in all likelihood, differ to the date our modern calendar recognises as the previous Dawn of Leo. It barely needs to be said but this start date or 'Year 0' is crucial to determine the dates encoded into the Precession Wheel. And it would seem that this crucial date is provided for us through the Great Giza Triangle. Let us now see how.
In the design of the GGT (and indeed the 3 Great Pyramids themselves) we are immediately drawn to the 'misaligned pyramid' of Menakau-Ra. It is one of Giza's most enduring puzzles and we find ourselves asking (as Robert Bauval did) why should this small pyramid be off-centre? Certainly the Centroid Alignment Theory shows how it comes to be misaligned from a mathematical perspective but it does not explain why the Designer's would have chosen such a design technique to 'create' such a misalignment. What is it they are trying to show us with this misalignment? What truth, if any, lies in the maths?
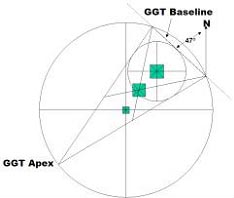
Figure 3c – Misalignment of Menkau-Ra is Due to 47 angle (from North) of the GGT Baseline
Mathematically, the misaligned pyramid of Menkau-Ra (in the context of the Centroid Alignment Theory) is misaligned specifically due to the angle of the GGT baseline (figure 3c). Changing the angle of the GGT baseline has the effect of shifting the position of Menkau-Ra's centre point. The baseline and the centre point (or centroid) of Menkau-Ra are, therefore, inextricably linked. In other words – the Designers' have fixed the baseline of the GGT at a very specific angle – 47 degrees from true north – in order to achieve the very specific misalignment of Menkau-Ra.
So now, if we are to accept (as Bauval/Gilbert propose) that the misaligned pyramid of Menkau-Ra is symbolic of the misaligned star (Mintaka) in Orion's Belt, then what can possibly connect this star with the 47 degrees we find in the Great Giza Triangle's baseline? The answer is simple and logical – declination!
The constellation of Orion (as with most constellations) slowly changes its declination (i.e. drifts up and down) on the southern horizon over the course of the Great Year (figure 3d). So, it is possible then that the fundamental purpose of the Great Giza Triangle is to provide us with a precise 'dating mechanism' for the astronomical clock based on the 'misaligned' star (Mintaka) with pyramid (Menkau-Ra). Let us take a moment to examine Mintaka's declination over the last 13,000 years.
| Year | Declination |
| 2,007AD | -0.50 |
| 2,007BC | -11.90 |
| 5,000BC | -27.90 |
| 7,500BC | -40.50 |
| 10,000BC | -47.27 |
| 10,950BC | -47.00 |
Figure 3d – Declination of Mintaka over the Ages (Source: Skyglobe 4)
Mintaka appears to have a declination of -47 in the year 10,950BC. Intriguingly, this date shows a remarkable correlation with other ancient sources that place the Dawn of Leo circa 10,948BC – a difference of only 2 years. We now have the start date (Year 0) of the Precession Wheel -10,948BC.
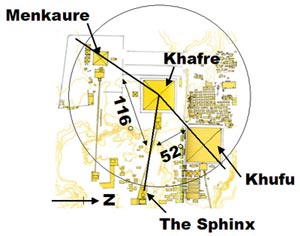
Figure 4 – The Sphinx Represents the Dawn of the Previous Age of Leo (10,948BC) Map Source, Lehner – `The Complete Pyramids’
It is a very simple calculation to convert the angle of these alignments into actual dates. Since we know that 1 degree of the Great Precession Year is equivalent to approximately 72 years, a simple multiplication yields the number of years for each angle:
Khufu alignment = 52° x 72 = 3,744 years + 10,948 (dawn of Leo) = 14,692BC (16,692BP)
Menkau-Ra Alignment = 116° * 72 = 8,352 years – 10,948 (dawn of Leo) = 2,596BC (4,596BP)
Intriguingly these 2 dates correspond with highly significant past events. It is a matter of scientific fact that around 16,000-17,000 years ago the end of the last ice age took place. The catalyst for this defining moment in the development of human civilisation still remains a mystery but it is perhaps possible that the ancient Designers allude to its cause within the Giza Precession Wheel.
The second date (the Menkau-Ra alignment) of 4,596BP is equally significant since this seems to point directly to the era within which Egyptologists believe the Giza pyramids were finally completed.
The Giza Oracle indicates a number of other dates that have been plainly encoded into the wheel and demonstrates how these dates also correlate with significant events from our ancient past, in particular, the global extinction event that took place around 13,000BP – a date that correlates almost perfectly with the Precession Wheel start year of 12,948BP. But more than this, it seems that the ancient Designers of the wheel are perhaps indicating that the events of the past are actually part of a cycle, a cycle that could possibly see a return to the events of the past some time in our immediate future.
The Giza Oracle
Author, Scott Creighton
Available from www.lulu.com
References:
Hamlet’s Mill – Giorgio De Santillana and Hertha Von Dechend
The Complete Pyramids – Mark Lehner
Kingdom of the Ark – Lorraine Evans
The Atlantis Blueprint – Rand Flem-Ath and Colin Wilson
The Orion Mystery – Robert Bauval and Adrian Gilbert
The search for the Stone of Destiny – Pat Gerber
When the Sky Fell – Rand and Rose Flem-Ath
Fingerprints of the Gods – Graham Hancock
Maps of the Ancient Sea Kings – Charles H. Hapgood
The Golden Thread of Time – Crichton E M Miller
The Hiram Key – Christopher Knight, Robert Lomas
Giza Plateau – www.Aiwaz.net/giza/ – Morphvs
Discussions in Egyptology – John Legon
Planet X – www.xfacts.com – Jason Martell
The Upuaut Project – Rudolf Gantenbrink
Robert Powell – The Definition of the Babylonian Zodiac and the Influence of Babylonian Astronomy on the Subsequent Defining of the Zodiac’






Please take this with repect to mathmatics. mathmatics can tell you what can be built , but only the builer can tell you how to build it . case in point fill a can of soda full of sand is the sand a soild becouse the can can’t be crushed this depends on if the builder wants to pour the sand out like water
whatI’M SAYING IS IF THEY BUILT THE PYRAMIDS 5 MILES IN A DIFFERENT DIERCTION CHANCES ARE THEY WOULD STILL BUILD THEM THE SAME WAY..Your explanation of the postion of the pyramids was cool I think I learned something
Alan Christ